This file was built on
- SageMath 8.6
- Jupyter 4.4.0
- CoCalc
Thanks to these softwares this lecture was made possible.
主題¶
- 一筆劃問題（Eulerian circuit）
- 多面體公式（Euler's polyhedron formula）
- 圖著色問題（Graph coloring problem）
- 搜尋演算法（Searching algorithm）
1. 一筆劃問題（Eulerian circuit）¶
李昂哈德·歐拉 Leonhard Euler (1707–1783)
(Portrait by Jakob Emanuel Handmann
Source: Wikipedia: Leonhard Euler)
在歐拉的時代
東普魯士的柯尼斯堡（Königsberg）
有條河流把城市切成兩岸，中間還有兩座大島
有七座橋連接著城市的交通
西元 1736 年，歐拉思考著以下的問題。
七橋問題：能不能經過這七座橋恰好一次，然後回到原點？
(Source: Wikipedia: Seven Bridges of Königsberg)
圖論中點的位置並不重要，邊怎麼畫也沒關係。
以下網頁可以繪製圖：
Radoslav Kirov's JavaScript Graph Editor.
V = [1,2,3,4] ### four vertices
E = [(1,2,'e1'),(1,2,'e2'),(1,3,'e3'),(1,3,'e4'),(1,4,'e5'),(2,4,'e6'),(3,4,'e7')] ### seven edges
pos = {1: (0,0), 2: (1,1), 3: (1,-1), 4: (2,0)}
G = Graph([V,E], multiedges=True, pos=pos)
G.show(figsize=[3,3],edge_labels=True)
G.eulerian_circuit()
False
V = [1,2,3,4] ### four vertices
E = [(1,2,'e1'),(1,2,'e2'),(1,3,'e3'),(1,3,'e4'),(2,3,'e5'),(2,4,'e6'),(3,4,'e7')] ### seven edges
pos = {1: (0,0), 2: (1,1), 3: (1,-1), 4: (2,0)}
H = Graph([V,E], multiedges=True, pos=pos)
H.show(figsize=[3,3],edge_labels=True)
H.eulerian_circuit()
[(1, 3, 'e4'), (3, 4, 'e7'), (4, 2, 'e6'), (2, 3, 'e5'), (3, 1, 'e3'), (1, 2, 'e2'), (2, 1, 'e1')]
### interactive function
### you have to open the notebook
### by Jupyter in order to see it
walk_on_graph(G)
定義¶
在一個圖上
路徑（walk）指的是一連串的邊 v1v2,v2v3,v3v4,…。
迴圈（closed walk）指的是繞了一圈又回到起點的一條路徑。
而一個圖 G 的歐拉迴圈（Eulerian circuit）是指
一條走過所有邊_恰好一次_的迴圈。
一筆劃問題：哪些圖擁有歐拉迴圈？有的話怎麼找？
觀察¶
如果一個圖有歐拉迴圈
那麼每個點的度數都必須是偶數。
結果¶
七橋問題中的圖並沒有歐拉迴圈。
定義¶
如果一個圖上任兩個點都有一條路徑相連
我們說這個圖是連通的（connected）。
sshow(graphs.CycleGraph(4),'connected')
sshow(graphs.CycleGraph(3).disjoint_union(graphs.CycleGraph(3)),'not connected')
觀察¶
如果一個圖有歐拉迴圈
那麼這個圖必須是連通的。
定理（Euler 1736）¶
如果一個連通的圖上
每個點的度數皆為偶數
那麼這個圖上就找得到歐拉迴圈。
試試看：在下方的圖中找一個歐拉迴圈。
g = Graph([five_V, sum(five_E,[])], pos=five_pos)
pic1 = g.plot(figsize=[3,3])
pic1.show()
不難找到！但是亳無策略地走不見得每次都成功。
center_walk = DiGraph([five_V,five_E[0]], pos=five_pos)
pic1 += center_walk.plot(figsize=[3,3], edge_color='red')
pic1.axes(False)
pic1.show(title='Not always work')
觀察¶
如果圖中每個點度數皆為偶數，
從任一點開始走，
遇到邊就往前走，
過程中一直都只有起點和終點的度數為奇數，
所以不能再走的時候
一定是回到起點，形成了一個迴圈。
觀察¶
如果圖 G 每個點度數皆為偶數
那麼在把某迴圈中的邊
都從 G 中去掉之後
新的圖中每個點度數依然皆為偶數。
@interact
### interactive function
def _(step=slider(list(range(10)))):
base = step // 2
has_walk = step % 2
base_graph = Graph([five_V,sum(five_E[base:],[])], pos=five_pos)
pic1 = base_graph.plot(figsize=[3,3])
if has_walk:
walk_graph = DiGraph([five_V,five_E[base]], pos=five_pos)
pic1 += walk_graph.plot(figsize = [3,3], edge_color = rainbow(5)[base])
pic1.axes(False)
pic1.show()
base_graph = Graph([five_V,sum(five_E,[])], pos=five_pos)
walk_graph = DiGraph([five_V,sum(five_E,[])], pos=five_pos)
pic1 = base_graph.plot(figsize=[3,3])
pic1 += walk_graph.plot(figsize = [3,3], edge_colors={rainbow(5)[k]: five_E[k] for k in range(5)} )
pic1.axes(False)
pic1.show()
歐拉定理的證明¶
前提：
- 圖 G 上每個點度數皆為偶數
- 圖 G 是連通的
演算法：
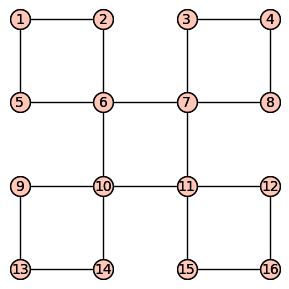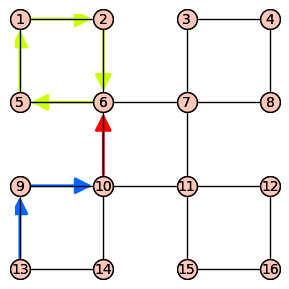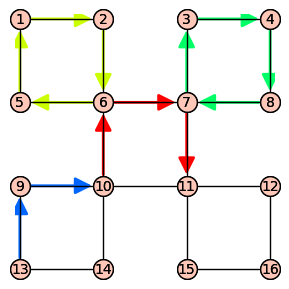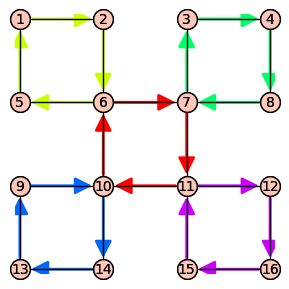
- 把圖 G 的邊分解成一堆迴圈 [By 前提 1]
- 從任一迴圈開始
- 當遇到沒碰過的迴圈時，先走新的迴圈
- 最終每個迴圈都會被走過 [By 前提 2]
- 這樣就找到一個歐拉迴圈了！
2. 多面體公式（Euler's polyhedron formula）¶
假設一個多面體有的點數為 V，邊數為 E，而面數為 F。
則 V−E+F=2。
@interact
### interactive function
def _(
faces = selector([4,6,8,12,20], buttons=True)
):
f_to_g = {4: graphs.TetrahedralGraph(), 6: graphs.HexahedralGraph(), 8: graphs.OctahedralGraph(), 12: graphs.DodecahedralGraph(), 20: graphs.IcosahedralGraph()}
g = f_to_g[faces]
print('V - E + F = {} - {} + {} = {}'.format(g.order(), g.size(), faces, g.order() - g.size() + faces))
g.plot3d().show()
結果¶
正多面體只有以下五種：
正四面體、正六面體、正八面體、正十二面體、正二十面體。
1. 面為正三角形
每個面有三條邊，每條邊碰到兩個面，所以 3F=2E⟹F=23E。
因為正三角形內角為 60∘，k 可以是 3,4,5。
1a. k=3
每個點碰到三條邊，每條邊碰到兩個點，所以 3V=2E⟹V=23E。
利用多面體公式
V−E+F=23E−E+23E=2
得到
2E−3E+2E=6⟹E=6。
因此 V=4,E=6,F=4： 正四面體。
1b. k=4
每個點碰到四條邊，每條邊碰到兩個點，所以 4V=2E⟹V=12E。
利用多面體公式
V−E+F=12E−E+23E=2
得到
3E−6E+4E=12⟹E=12。
因此 V=6,E=12,F=8： 正八面體。
1c. k=5
每個點碰到五條邊，每條邊碰到兩個點，所以 5V=2E⟹V=25E。
利用多面體公式
V−E+F=25E−E+23E=2
得到
6E−15E+10E=30⟹E=30。
因此 V=12,E=30,F=20： 正二十面體。
2. 面為正方形
每個面有四條邊，每條邊碰到兩個面，所以 4F=2E⟹F=12E。
因為正方形內角為 90∘，k 只能是 3。
這樣的話，每個點碰到三條邊，每條邊碰到兩個點，所以 3V=2E⟹V=23E。
利用多面體公式
V−E+F=23E−E+12E=2
得到
4E−6E+3E=12⟹E=12。
因此 V=8,E=12,F=6： 正六面體。
3. 面為正五邊形
每個面有五條邊，每條邊碰到兩個面，所以 5F=2E⟹F=25E。
因為正五邊形內角為 108∘，k 只能是 3。
這樣的話，每個點碰到三條邊，每條邊碰到兩個點，所以 3V=2E⟹V=23E。
利用多面體公式
V−E+F=23E−E+25E=2
得到
10E−15E+6E=30⟹E=30。
因此 V=20,E=30,F=12： 正十二面體。
搞定～！
定義¶
一個圖若可以畫在平面上
且邊都沒有交叉
則稱為一個平面圖（planar graph）。
觀察¶
每一個多面體的圖都是平面圖。
每一個圈圖（cycle）都是平面圖。
multi_sshow([graphs.CycleGraph(k).graph6_string() for k in range(3,8)])
定理¶
假設 G 是一個連通的圖且包含至少一個圈。
若 G 被畫在平面上且邊無交叉時
有 V 個點，E 條邊，以及 F 個面，
那麼 V−E+F=2。
觀察¶
一個 n 個點的圈圖符合 V−E+F=n−n+2=2。
觀察¶
假設圖 G 滿足定理所有條件。
那麼 G 可以從圈圖開始，並只用以下兩種動作建構出來：
- 新增一個點並將這個點連到原先的某一點
- 新增一條邊
試試看：Radoslav Kirov's JavaScript Graph Editor。
定理證明¶
數學歸納法！
動作 1:
V′=V+1, E′=E+1, F′=F
所以 V′−E′+F′=(V+1)−(E+1)+F=2。
動作 2:
V′=V, E′=E+1, F′=F+1
所以 V′−E′+F′=V−(E+1)+(F+1)=2。
搞定～！
3. 圖著色問題（Graph coloring problem）¶
軼事：
Francis Guthrie 在 1852 年時發現英格蘭的地圖可以只用四種顏色著色。
Francis 跟他弟弟 Frederick 說，他弟弟跟他指導教授 Augustus De Morgan 說。
四色問題： 是不是每一張地圖都可以只用_四種顏色_著色，且相鄰地區不同色？
很多人嘗試回答這個問題：
Alfred Kempe 在 1879 提出一個證明；
Peter Guthrie Tait 在 1880 提出另一個證明。
Percy Heawood 在 1890 發現 Kempe 的證明有錯；
Julius Petersen 在 1891 發現 Tait 的證明有錯。
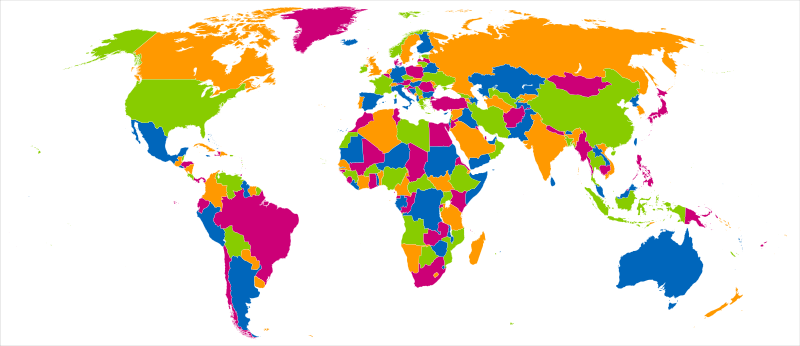
(Source: Wikipedia: Four color theorem)
(Source: Wikipedia: Four color theorem)
藉由地圖和平面圖的轉換，可以改寫原本的問題。
四色問題：是不是每一個平面圖的點都可以只用_四種顏色_著色，且相鄰點不同色？
每個正多面體的圖都可以用四種顏色著色。
### interactive function
g = graphs.TetrahedralGraph()
g.set_pos({0:(0,0), 1:(0,1), 2:(0.8,-0.5), 3:(-0.8,-0.5)})
illustrate_FS(g,0,'BFS',searching_tree=False,coloring=True)
### interactive function
g = graphs.HexahedralGraph()
g.set_pos({0:(0,3), 1:(3,3), 2:(3,0), 3:(0,0), 4:(1,2), 5:(2,2), 6:(2,1), 7:(1,1)})
illustrate_FS(g,0,'BFS',searching_tree=False,coloring=True)
### interactive function
g = graphs.OctahedralGraph()
illustrate_FS(g,0,'BFS',searching_tree=False,coloring=True)
### interactive function
g = graphs.DodecahedralGraph()
illustrate_FS(g, 0, 'BFS', searching_tree=False, coloring=True)
g = graphs.IcosahedralGraph()
g.show(vertex_colors=g.coloring(hex_colors=True))
g = graphs.DodecahedralGraph()
g.show(vertex_colors=g.coloring(hex_colors=True))
四色定理（Robertson, Sanders, Seymour, and Thomas 1997）¶
任何平面圖都能用四種顏色將點著色，且相鄰點不同色。
四色定理的證明仰賴大量電腦計算。
4. 搜尋演算法（Searching algorithm）¶
圖上的搜尋演算法
目的是在圖上有系統地搜尋所有點（或是邊、或是都找）。
以下是兩種常見的搜尋演算法：
- 深度優先搜尋 Depth-first search（DFS）
- 廣度優先搜尋 Breadth-first search（BFS）
下方的圖叫作 Petersen graph。
g = graphs.PetersenGraph()
g.show()
### interactive function
g = graphs.PetersenGraph()
v = 0
illustrate_FS(g, v, 'DFS')
### interactive function
g = graphs.PetersenGraph()
v = 0
illustrate_FS(g, v, 'BFS')
貪婪著色演算法¶
圖的點要給定一個順序。
依照這個順序一一著色，
著色時能不用新顏色就不用新顏色。
### interactive function
g = graphs.PetersenGraph()
v = 0
illustrate_FS(g, v, 'BFS', coloring=True)
### interactive function
g = graphs.PetersenGraph()
v = 0
illustrate_FS(g, v, 'DFS', coloring=True)
不同的點的順序會決定著出來的顏色。
定義¶
若 G 是一個圖，
Δ(G) 代表的是圖上的最大度數，而
δ(G) 代表的是圖上的 最小度數。
觀察¶
貪婪著色演算法（任何的點的順序都行）至多用到 Δ(G)+1 種顏色。
所以 χ(G)≤Δ(G)+1。
當圖是奇圈（odd cycle） C2k+1 時：
Δ(C2k+1)=2
χ(C2k+1)=2+1=3
g = graphs.CycleGraph(5)
illustrate_FS(g, 0, 'DFS', searching_tree=False, coloring=True)
當圖是完全圖（complete graph） Kn 時：
Δ(Kn)=n−1
χ(Kn)=n−1+1=n
g = graphs.CompleteGraph(5)
g.show(vertex_colors=g.coloring(hex_colors=True))
Brook's theorem¶
若一個圖不是奇圈也不是完全圖，
則 χ(G)≤Δ(G)。
Brook's theorem 的證明仰賴 DFS。